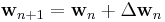Adaptive filter
An adaptive filter is a filter that self-adjusts its transfer function according to an optimization algorithm driven by an error signal. Because of the complexity of the optimization algorithms, most adaptive filters are digital filters. By way of contrast, a non-adaptive filter has a static transfer function. Adaptive filters are required for some applications because some parameters of the desired processing operation (for instance, the locations of reflective surfaces in a reverberant space) are not known in advance. The adaptive filter uses feedback in the form of an error signal to refine its transfer function to match the changing parameters.
Generally speaking, the adaptive process involves the use of a cost function, which is a criterion for optimum performance of the filter, to feed an algorithm, which determines how to modify filter transfer function to minimize the cost on the next iteration.
As the power of digital signal processors has increased, adaptive filters have become much more common and are now routinely used in devices such as mobile phones and other communication devices, camcorders and digital cameras, and medical monitoring equipment.
Contents |
Example application
Suppose a hospital is recording a heart beat (an ECG), which is being corrupted by a 50 Hz noise (the frequency coming from the power supply in many countries). However, due to slight variations in the power supply to the hospital, the noise signal may contain harmonics of the noise and the exact frequency of the noise may vary.
One way to remove the noise is to filter the signal with a notch filter at 50 Hz. Such a static filter would need to remove all the frequencies in the vicinity of 50 Hz, which could excessively degrade the quality of the ECG since the heart beat would also likely have frequency components in the rejected range.
To circumvent this potential loss of information, an adaptive filter could be used. The adaptive filter would take input both from the patient and from the power supply directly and would thus be able to track the actual frequency of the noise as it fluctuates. Such an adaptive technique generally allows for a filter with a smaller rejection range, which means, in our case, that the quality of the output signal is more accurate for medical diagnoses.
Block diagram
The block diagram, shown in the following figure, serves as a foundation for particular adaptive filter realisations, such as Least Mean Squares (LMS) and Recursive Least Squares (RLS). The idea behind the block diagram is that a variable filter extracts an estimate of the desired signal.
To start the discussion of the block diagram we take the following assumptions:
- The input signal is the sum of a desired signal
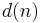 and interfering noise
and interfering noise 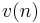
- The variable filter has a Finite Impulse Response (FIR) structure. For such structures the impulse response is equal to the filter coefficients. The coefficients for a filter of order
 are defined as
are defined as
![\mathbf{w}_{n}=\left[w_{n}(0),\,w_{n}(1),\, ...,\,w_{n}(p)\right]^{T}](/2012-wikipedia_en_all_nopic_01_2012/I/c150085d7e0c9358af6ba9282af46a28.png) .
.
- The error signal or cost function is the difference between the desired and the estimated signal
The variable filter estimates the desired signal by convolving the input signal with the impulse response. In vector notation this is expressed as
where
is an input signal vector. Moreover, the variable filter updates the filter coefficients at every time instant
where 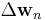 is a correction factor for the filter coefficients. The adaptive algorithm generates this correction factor based on the input and error signals. LMS and RLS define two different coefficient update algorithms.
is a correction factor for the filter coefficients. The adaptive algorithm generates this correction factor based on the input and error signals. LMS and RLS define two different coefficient update algorithms.
Applications of adaptive filters
Filter implementations
- Least mean squares filter
- Recursive least squares filter
- Multidelay block frequency domain adaptive filter
See also
- Kalman filter
- Wiener filter
- Linear prediction
- Filter (signal processing)
- Kernel adaptive filter
- Wiener-Hopf equation
References
- Monson H. Hayes Statistical Digital Signal Processing and Modeling, Wiley, 1996, ISBN 0-471-59431-8
- Simon Haykin Adaptive Filter Theory, Prentice Hall, 2002, ISBN 0-13-048434-2
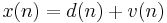
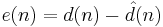
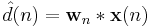
![\mathbf{x}(n)=\left[x(n),\,x(n-1),\,...,\,x(n-p)\right]^{T}](/2012-wikipedia_en_all_nopic_01_2012/I/33419c642f6bbf163193ab84201a5a31.png)